21 - 24 Solved problems in maxima and minima

Diameter D is constant (circle is given)
$x^2 + y^2 = D^2$

$2x + 2y \, y' = 0$

$y' = -x/y$
 

Perimeter
$P = 2x + 2y$

$dP/dx = 2 + 2y' = 0$

$2 + 2(-x/y) = 0$

$y = x$
 

The largest rectangle is a square.           answer
 

See also the solution using trigonometric function.

$x^2 + y^2 = c^2$

$2x + 2y \, y' = 0$

$y' = -x/y$
 

Area:
$A = \frac{1}{2} xy$

$dA/db = \frac{1}{2} \, [ \, x y' + y \, ] = 0$

$x y' + y = 0$

$x (-x/y) + y = 0$

$y = x^2 / y$

$y^2 = x^2$

$y = x$
 

The triangle is an isosceles right triangle.           answer

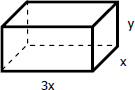
Given Volume:
$V = x \, (3x) \, y

V = 3x^2 \, y$

$0 = 3x^2 \, y' + 6xy$

$y' = -2y/x$
 

Total Area:
$A_T = 2(3x^2) + 2(3xy) + 2(xy)$

$A_T = 6x^2 + 8xy$

$dA_T / dx = 12x + 8 \, (x y' + y) = 0$

$12x + 8 \, [ \, x (-2y/x) + y \, ] = 0$

$12x + 8 \, [ \, -2y + y \, ] = 0$

$12x = 8y$

$y = \frac{3}{2} x$
 

Altitude = 3/2 × shorter side of base.           answer

Given Volume:
$V = x \, (3x) \, y$

$V = 3x^2 \, y$

$0 = 3x^2 \, y' + 6xy$

$y' = -2y/x$
 

Area:
$A = 3x^2 + 2(3xy) + 2(xy)$

$A = 3x^2 + 8xy$

$dA/dx = 6x + 8(x \, y' + y) = 0$

$6x + 8 \, [ \, x (-2y/x) + y \, ] = 0$

$6x + 8 \, [ \, -2y + y \, ] = 0$

$6x = 8y$

$y = \frac{3}{4}x$
 

Altitude = 3/4 × shorter side of base.           answer