Types of Annuities

Contents

  1. Ordinary Annuity
  2. Annuity Due
  3. Deferred Annuity
  4. Perpetuity

Types of Simple Annuities
In engineering economy, annuities are classified into four categories. These are: (1) ordinary annuity, (2) annuity due, (3) deferred annuity, and (4) perpetuity. These four are actually simple annuities described in the previous page.
 

Back to top

Ordinary Annuity

In ordinary annuity, the equal payments are made at the end of each compounding period starting from the first compounding period.
 

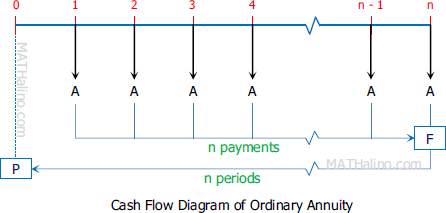
000-ordinary-annuity-cash-flow.gif

 

From the cash flow diagram shown above, the future amount F is the sum of payments starting from the end of the first period to the end of the nth period. Observe that the total number of payments is n and the total number of compounding periods is also n. Thus, in ordinary annuity, the number of payments and the number of compounding periods are equal.
 

Future amount of ordinary annuity, F

$F = \dfrac{A[ \, (1 + i)^n - 1 \, ]}{i}$

The factor   $\dfrac{(1 + i)^n - 1}{i}$   is called equal-payment-series compound-amount factor and is denoted by   $(F/A, \, i, \, n)$.
 

Present amount of ordinary annuity, P

$P = \dfrac{F}{(1 + i)^n} = \dfrac{A[ \, (1 + i)^n -1 \, ]}{(1 + i)^ni}$

The factor   $\dfrac{(1 + i)^n - 1}{(1 + i)^ni}$   is called equal-payment-series present-worth factor and is denoted by   $(P/A, \, i, \, n)$.
 

Periodic payment of annuity, A
Value of A if F is known:

$A = \dfrac{Fi}{(1 + i)^n - 1}$

The factor   $\dfrac{i}{(1 + i)^n - 1}$   is called equal-payment-series sinking-fund factor and is denoted by   $(A/F, \, i, \, n)$.
 

Value of A if P is known:

$A = \dfrac{P(1 + i)^ni}{(1 + i)^n - 1}$

The factor   $\dfrac{(1 + i)^ni}{(1 + i)^n - 1}$   is called equal-payment-series capital-recovery factor and is denoted by   $(A/P, \, i, \, n)$.
 

Back to top

Annuity Due

In annuity due, the equal payments are made at the beginning of each compounding period starting from the first period. The diagram below shows the cash flow in annuity due.
 

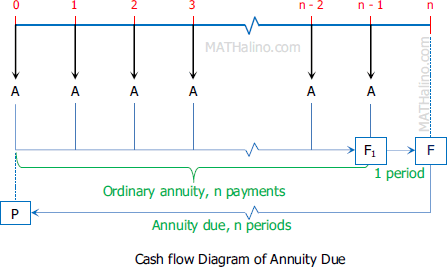
Cash flow of annuity due

 

As indicated in the figure above, F1 is the sum of ordinary annuity of n payments. The future amount F of annuity due at the end of nth period is one compounding period away from F1. In symbol, F = F1(1 + i).
 

Future amount of annuity due, F

$F = F_1(1 + i) = \dfrac{A[ \, (1 + i)^n -1 \, ]}{i}(1 + i)$

 

Present amount of annuity due, P

$P = \dfrac{F}{(1 + i)^n} = \dfrac{A[ \, (1 + i)^n -1 \, ]}{(1 + i)^ni}(1 + i)$

 

Back to top

Deferred Annuity

In deferred annuity the first payment is deferred a certain number of compounding periods after the first. In the diagram below, the first payment was made at the end of the kth period and n number of payments was made. The n payments form an ordinary annuity as indicated in the figure.
 

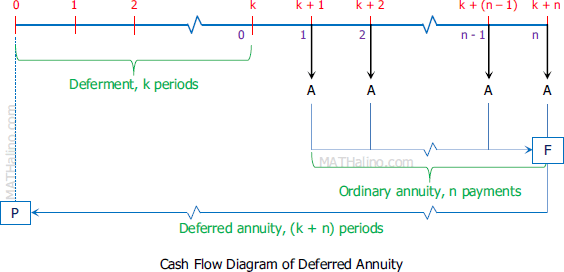
000-deferred-annuity-cash-flow.gif

 

Future amount of deferred annuity, F

$F = \dfrac{A[ \, (1 + i)^n -1 \, ]}{i}$

 

Present amount of deferred annuity, P

$P = \dfrac{F}{(1 + i)^{k + n}} = \dfrac{A[ \, (1 + i)^n -1 \, ]}{(1 + i)^{k + n}i}$

 

Back to top

Perpetuity

Perpetuity is an annuity where the payment period extends forever, which means that the periodic payments continue indefinitely.
 

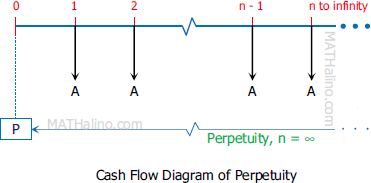
Cash flow diagram of perpetuity

 

There is no definite future in perpetuity, thus, there is no formula for the future amount.
 

Present amount of perpetuity, P
From the present amount of ordinary annuity:
$P = \dfrac{A[ \, (1 + i)^n -1 \, ]}{(1 + i)^ni}$

$P = \dfrac{A(1 + i)^n}{(1 + i)^ni} - \dfrac{A}{(1 + i)^ni}$

$P = \dfrac{A}{i} - \dfrac{A}{(1 + i)^ni}$
 

When   $n \to \infty$,   $\dfrac{A}{(1 + i)^ni} \to 0$.   Thus,

$P = \dfrac{A}{i}$

 

Back to top
Tags
deferred annuity
ordinary annuity
simple annuity
perpetuity
annuity due