Solution to Problem 417 | Shear and Moment Diagrams | Strength of Materials Review at MATHalino

Problem 417
Beam carrying the triangular loading shown in Fig. P-417.

Click here to read or hide the general instruction

Write shear and moment equations for the beams in the following problems. In each problem, let x be the distance measured from left end of the beam. Also, draw shear and moment diagrams, specifying values at all change of loading positions and at points of zero shear. Neglect the mass of the beam in each problem.

Solution 417

Click here to expand or collapse this section

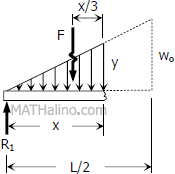
By symmetry:
$R_1 = R_2 = \frac{1}{2}(\frac{1}{2}Lw_o) = \frac{1}{4}Lw_o$

$\dfrac{y}{x} = \dfrac{w_o}{L/2}$

$y = \dfrac{2w_o}{L}x$

$F = \frac{1}{2}xy = \frac{1}{2}x \left( \dfrac{2w_o}{L} \right)$

$F = \dfrac{w_o}{L}x^2$

$V = R_1 - F$

$V = \frac{1}{4}Lw_o - \dfrac{w_o}{L}x^2$

$M = R_1x - F(\frac{1}{3}x)$

$M = \frac{1}{4}Lw_ox - \left( \dfrac{w_o}{L}x^2 \right)(\frac{1}{3}x)$

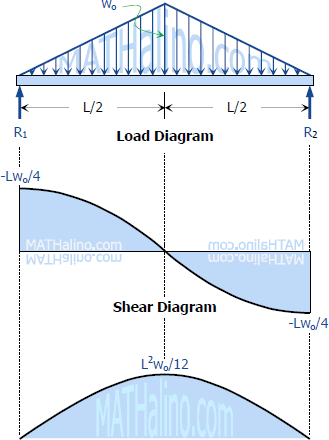To draw the Shear Diagram:
V = Lw_o/4 - w_ox²/L is a second degree curve; at x = 0, V = Lw_o/4; at x = L/2, V = 0. The other half of the diagram can be drawn by the concept of symmetry.

To draw the Moment Diagram
M = Lw_ox/4 - w_ox₃/3L is a third degree curve; at x = 0, M = 0; at x = L/2, M = L₂w_o/12. The other half of the diagram can be drawn by the concept of symmetry.

Solution to Problem 417 | Shear and Moment Diagrams

Navigation

Recent comments