028 Review Problem - Amount of metal sheet used to construct a water tank

$V = 10,000 ~ \tetx{gal.} \times \dfrac{231 ~ \text{in.}^3}{1 ~ \text{gal.}} \times \left( \dfrac{1 ~ \text{ft.}}{12 ~ \text{in.}} \right)^3$

$V = 1336.806 ~ \text{ft.}^3$
 

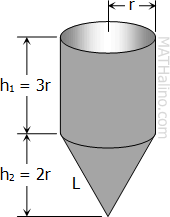$V_{cylinder} + V_{cone} = V$

$\pi r^2 h_1 + \frac{1}{3}\pi r^2 h_2 = V$

$\pi r^2(3r) + \frac{1}{3}\pi r^2(2r) = 1336.806$

$\frac{11}{3}\pi r^3 = 1336.806$

$r = 4.878 \, \text{ft.}$
 

$h_1 = 3(4.878) = 14.634 ~ \text{ft.}$

$h_2 = 2(4.878) = 9.756 ~ \text{ft.}$
 

$A = A_{L-cylinder} + A_{L-cone}$

$A = 2\pi rh_1 + \pi rL$

$A = 2\pi(4.878)(14.634) + \pi(4.878)\sqrt{4.878^2 + 9.756^2}$

$A = 615.68 ~ \text{ft.}^2$           answer