The lines that trace the center of the spheres will form into square pyramid. See figure below.
From the pyramid shown to the right:
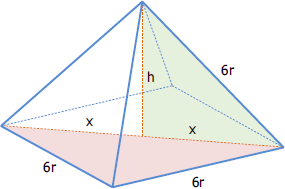 $(2x)^2 = (6r)^2 + (6r)^2$
$(2x)^2 = (6r)^2 + (6r)^2$
$(2x)^2 = 2(36r^2)$
$2x = 6r\sqrt{2}$
$x = 3r\sqrt{2}$
$x^2 = 9r^2(2)$
$x^2 = 18r^2$
$h^2 + x^2 = (6r)^2$
$h^2 + 18r^2 = 36r^2$
$h^2 = 18r^2$
$h^2 = (9r^2)(2)$
 $h = 3r\sqrt{2}$
$h = 3r\sqrt{2}$
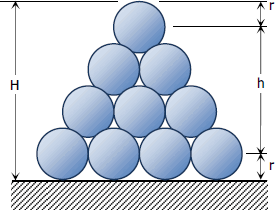
Total height of the pile
$H = 2r + h$
$H = 2r + 3r\sqrt{2}$
$H = (2 + 3\sqrt{2})r$ answer