Frustum of a Right Circular Cone
Frustum of a right circular cone is that portion of right circular cone included between the base and a section parallel to the base not passing through the vertex.
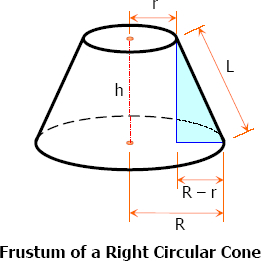
Properties of Frustum of Right Circular Cone
- The altitude of a frustum of a right circular cone is the perpendicular distance between the two bases. It is denoted by h.
- All elements of a frustum of a right circular cone are equal. It is denoted by L.
Formulas for Frustum of Right Circular Cone
$A_1 = \pi R^2$
$A_2 = \pi r^2$
The lateral area of the frustum of a right circular cone is equal to one-half the sum of the circumference of the bases multiplied by slant height. See the derivation of the formula for lateral area of frustum of a right circular cone.
Let C and c, the circumference of lower and upper bases, respectively.
$A_L = \frac{1}{2}(C + c)L$
A more convenient formula is when we substitute C = 2πR and c = 2πr, giving us
$A_L = \pi (R + r) L$
The volume of a frustum of any cone is equal to one-third of the product of the altitude and the sum of the upper base, the lower base, and the mean proportional between the two bases. See the derivation of formula for the volume of any frustum.
For any Frustum, the volume is $V = \frac{1}{3}\left( A_1 + A_2 + \sqrt{A_1 A_2} \right) h$. For frustum of right circular cone, $A_1 = \pi R^2$ and $A_2 = \pi r^2$. Thus,
$V = \frac{1}{3}\left[ \pi R^2 + \pi r^2 + \sqrt{\pi R^2 (\pi r^2)} \right] h$
$V = \frac{1}{3} \left[ \pi R^2 + \pi r^2 + \pi Rr \right] h$
$V = \frac{1}{3}\pi (R^2 + r^2 + Rr)h$
The relationship between the lower base radius R, upper base radius r, altitude h, and element L is given by
$(R - r)^2 + h^2 = L^2$
- Add new comment
- 57065 reads
