Plane Trigonometry

The Six Trigonometric Functions

1.   $\sin \theta = \dfrac{a}{c}$

2.   $\cos \theta = \dfrac{b}{c}$

3.   $\tan \theta = \dfrac{a}{b}$

4.   $\csc \theta = \dfrac{c}{a}$

5.   $\sec \theta = \dfrac{c}{b}$

6.   $\cot \theta = \dfrac{b}{a}$

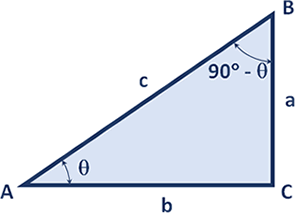
right-triangle-abc-theta.gif

 

Complementary Identities

1.   $\sin \theta = \cos (90^\circ - \theta)$

2.   $\cos \theta = \sin (90^\circ - \theta)$

3.   $\tan \theta = \cot (90^\circ - \theta)$

4.   $\cot \theta = \tan (90^\circ - \theta)$

5.   $\sec \theta = \csc (90^\circ - \theta)$

6.   $\csc \theta = \sec (90^\circ - \theta)$

 

Fundamental Identities

1.   $\sin \theta = \dfrac{1}{\csc \theta}$

2.   $\cos \theta = \dfrac{1}{\sec \theta}$

3.   $\tan \theta = \dfrac{1}{\cot \theta} = \dfrac{\sin \theta}{\cos \theta}$

4.   $\cot \theta = \dfrac{1}{\tan \theta} = \dfrac{\cos \theta}{\sin \theta}$

5.   $\sec \theta = \dfrac{1}{\cos \theta}$

6.   $\csc \theta = \dfrac{1}{\sin \theta}$

 

Pythagorean Theorem

$a^2 + b^2 = c^2$

 

Pythagorean Relations

1.   $\sin^2 \theta + \cos^2 \theta = 1$

2.   $\tan^2 \theta + 1 = \sec^2 \theta$

3.   $1 + \cot^2 \theta = \csc^2 \theta$

 

Sum of Two Angles

1.   $\sin (A + B) = \sin A \, \cos B + \cos A \, \sin B$

2.   $\cos (A + B) = \cos A \, \cos B - \sin A \, \sin B$

3.   $\tan (A + B) = \dfrac{\tan A + \tan B}{1 - \tan A \, \tan B}$

 

Difference of Two Angles

1.   $\sin (A - B) = \sin A \, \cos B - \cos A \, \sin B$

2.   $\cos (A - B) = \cos A \, \cos B + \sin A \, \sin B$

3.   $\tan (A - B) = \dfrac{\tan A - \tan B}{1 + \tan A \, \tan B}$

 

Double Angle Formulas

1.   $\sin 2\theta = 2 \sin \theta \, \cos \theta$

2.   $\cos 2\theta = \cos^2 \theta - \sin^2 \theta$

        2a.   $\cos 2\theta = 1 - 2\sin^2 \theta$

        2b.   $\cos 2\theta = 2\cos^2 \theta - 1$

3.   $\tan 2\theta = \dfrac{2\tan \theta}{1 - \tan^2 \theta}$

 

Half Angle Formulas

1.   $\sin \frac{1}{2}\theta = \sqrt{\dfrac{1 - \cos \theta}{2}}$

2.   $\cos \frac{1}{2}\theta = \sqrt{\dfrac{1 + \cos \theta}{2}}$

3.   $\tan \frac{1}{2}\theta = \dfrac{1 - \cos \theta}{\sin \theta} = \dfrac{\sin \theta}{1 + \cos \theta} = \sqrt{\dfrac{1 - \cos \theta}{1 + \cos \theta}}$

 

Powers of Functions

1.   $\sin^2 \theta = \frac{1}{2}(1 - \cos 2\theta)$

2.   $\cos^2 \theta = \frac{1}{2}(1 + \cos 2\theta)$

3.   $\tan^2 \theta = \dfrac{1 - \cos 2\theta}{1 + \cos 2\theta}$

 

Product of Functions

1.   $\sin A \, \cos B = \frac{1}{2} \big[ \sin (A + B) + \sin (A - B) \big]$

2.   $\sin A \, \sin B = \frac{1}{2} \big[ \cos (A - B) - \cos (A + B) \big]$

3.   $\cos A \, \cos B = \frac{1}{2} \big[ \cos (A + B) + \cos (A - B) \big]$

 

Sum of Functions

1.   $\sin A + \sin B = 2 \sin \frac{1}{2}(A + B) \, \cos \frac{1}{2}(A - B)$

2.   $\cos A + \cos B = 2 \cos \frac{1}{2}(A + B) \, \cos \frac{1}{2}(A - B)$

3.   $\tan A + \tan B = \dfrac{\sin (A + B)}{\cos A \, \cos B}$

 

Difference of Functions

1.   $\sin A - \sin B = 2 \sin \frac{1}{2}(A - B) \, \cos \frac{1}{2}(A + B)$

2.   $\cos A - \cos B = -2 \sin \frac{1}{2}(A + B) \, \sin \frac{1}{2}(A - B)$

3.   $\tan A - \tan B = \dfrac{\sin (A - B)}{\cos A \, \cos B}$

 

Sine Law

$\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}$

 

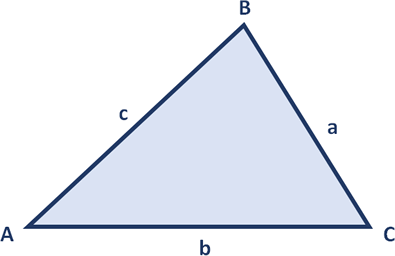
oblique-triangle-abc.gif

 

Cosine Law

1.   $a^2 = b^2 + c^2 - 2bc \cos A$

2.   $b^2 = a^2 + c^2 - 2ac \cos B$

3.   $c^2 = a^2 + b^2 - 2ab \cos C$

 

Law of Tangents

1.   $\dfrac{a - b}{a + b} = \dfrac{\tan \frac{1}{2}(A - B)}{\tan \frac{1}{2}(A + B)}$

2.   $\dfrac{b - c}{b + c} = \dfrac{\tan \frac{1}{2}(B - C)}{\tan \frac{1}{2}(B + C)}$

3.   $\dfrac{c - a}{c + a} = \dfrac{\tan \frac{1}{2}(C - A)}{\tan \frac{1}{2}(C + A)}$

 

Mollweide's Equations

1.   $\dfrac{a + b}{c} = \dfrac{\cos \frac{1}{2}(A - B)}{\sin \frac{1}{2}C}$

2.   $\dfrac{a - b}{c} = \dfrac{\sin \frac{1}{2}(A - B)}{\cos \frac{1}{2}C}$