Spherical Trigonometry

Spherical Triangle
Any section made by a cutting plane that passes through a sphere is circle. A great circle is formed when the cutting plane passes through the center of the sphere. Spherical triangle is a triangle bounded by arc of great circles of a sphere.
 

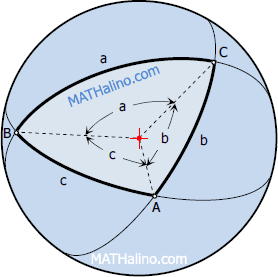
000-spherical-triangle-definition.gif

 

Note that for spherical triangles, sides a, b, and c are usually in angular units. And like plane triangles, angles A, B, and C are also in angular units.
 

Sum of interior angles of spherical triangle
The sum of the interior angles of a spherical triangle is greater than 180° and less than 540°.

$180^\circ \lt (A + B + C) \lt 540^\circ$

 

Area of spherical triangle
The area of a spherical triangle on the surface of the sphere of radius R is given by the formula

$A = \dfrac{\pi R^2E}{180^\circ}$

Where E is the spherical excess in degrees.
 

Spherical excess

$E = A + B + C - 180^\circ$

or

$\tan \frac{1}{4}E = \sqrt{\tan \frac{1}{2}s~\tan \frac{1}{2}(s - a)~\tan \frac{1}{2}(s - b)~\tan \frac{1}{2}(s - c)}$

Where $s = \frac{1}{2}(a + b + c)$
 

Spherical defect

$D = 360^\circ - (a + b + c)$

 

Note:
In spherical trigonometry, earth is assumed to be a perfect sphere. One minute (0° 1') of arc from the center of the earth has a distance equivalent to one (1) nautical mile (6080 feet) on the arc of great circle on the surface of the earth.

1 minute of arc = 1 nautical mile
1 nautical mile = 6080 feet
1 statute mile = 5280 feet
1 knot = 1 nautical mile per hour

 

Tags
great circle
spherical triangle
spherical excess
nautical mile
spherical defect