Right Spherical Triangle
Solution of right spherical triangle
With any two quantities given (three quantities if the right angle is counted), any right spherical triangle can be solved by following the Napier’s rules. The rules are aided with the Napier’s circle. In Napier’s circle, the sides and angle of the triangle are written in consecutive order (not including the right angle), and complimentary angles are taken for quantities opposite the right angle.
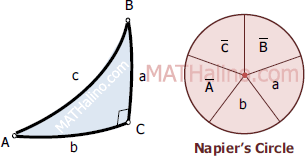 $\bar{A} = 90^\circ - A$
$\bar{A} = 90^\circ - A$
$\bar{B} = 90^\circ - B$
$\bar{c} = 90^\circ - c$
Napier’s Rules
SIN-COOP Rule
In the Napier’s circle, the sine of any middle part is equal to product of the cosines of its opposite parts.
If we take $a$ as the middle part, its opposite parts are $\bar{c}$ and $\bar{A}$, then by sin-coop rule
$\sin a = \cos \bar{c}~\cos \bar{A}$
$\sin a = \cos (90^\circ - c)~\cos (90^\circ - A)$
$\sin a = \sin c~\sin A$
SIN-TAAD Rule
In the Napier’s circle, the sine of any middle part is equal to the product of the tangents of its adjacent parts.
If we take $a$ as the middle part, the adjacent parts are $b$ and $\bar{B}$, then by sin-taad rule
$\sin a = \tan b~\tan \bar{B}$
$\sin a = \tan b~\tan (90^\circ - B)$
Spherical triangle can have one or two or three 90° interior angle. Spherical triangle is said to be right if only one of its included angle is equal to 90°. Triangles with more than one 90° angle are oblique.
- Log in to post comments

Please can you explain your
Please can you explain your notation; what does the horizontal line above some of the variables mean? I assume it signifies a line segment and not mean value? So what is the difference between, say, variable A and A with a bar? Thanks
Angle A with bar is the
In reply to Please can you explain your by Gareth (not verified)
Angle A with bar is the compliment of angle A without bar.
$\bar{A} = 90^\circ - A$