Conic Sections
Definition
Conic sections can be defined as the locus of point that moves so that the ratio of its distance from a fixed point called the focus to its distance from a fixed line called the directrix is constant. The constant ratio is called the eccentricity of the conic.
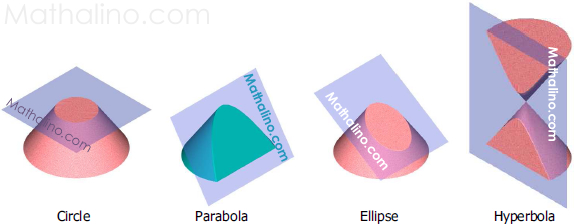
Conic sections are obtained by passing a cutting plane to a right circular cone. If the cutting plane is parallel to the base of the cone (or perpendicular to the axis of the cone), a circle is defined. If the cutting plane is parallel to lateral side (or generator) of the cone, parabola is defined. For a cutting plane that is oblique to the cone (not parallel nor perpendicular to any element), ellipse is defined. For a cutting plane parallel to the axis of the cone not passing through the vertex, the section formed is hyperbola. These were characterized by the Greek mathematician Apollonius (262 B.C. – 200 B.C.).
Equation of Conic Sections
The equation of general conic-sections is in second-degree,
The quantity B2 - 4AC is called discriminant and its value will determine the shape of the conic.
- If C = A and B = 0, the conic is a circle.
- If B2 - 4AC = 0, the conic is a parabola.
- If B2 - 4AC < 0, the conic is an ellipse.
- If B2 - 4AC > 0, the conic is a hyperbola.
The product xy would have a conic with axis oblique to the coordinate axes. If B = 0, the axis of the conic is parallel to one of the coordinate axes. As of now, our concern are for conics with axis parallel to one of the coordinate axes, thus B = 0. The equation then becomes
Eccentricity of Conic
Eccentricity is a measure of how much a conic deviate from being circular, making the eccentricity of the circle obviously equal to zero. It is the ratio of focal distance to directrix distance of the conic section.
- If e = 0, the conic is a circle.
- If e = 1, the conic is a parabola.
- If e < 1, the conic is an ellipse.
- If e > 1, the conic is a hyperbola.
- Log in to post comments
