Length of Arc in Polar Plane | Applications of Integration

Recall the relationship between polar and rectangular coordinates:
$x = r \cos \theta$   ←   Equation (1)

$y = r \sin \theta$   ←   Equation (2)
 

Differentiate both sides of Equations (1) and (2) in terms of θ
$\dfrac{dx}{d\theta} = \dfrac{dr}{d\theta} \cos \theta - r\sin \theta$

$\dfrac{dy}{d\theta} = \dfrac{dr}{d\theta} \sin \theta + r\cos \theta$
 

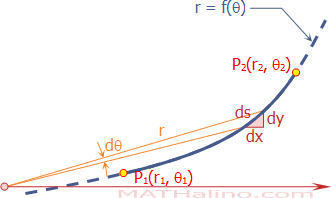
From the triangular strip shon in the figure:
$(ds)^2 = (dx)^2 + (dy)^2$

$\left( \dfrac{ds}{d\theta} \right)^2 = \left( \dfrac{dx}{d\theta} \right)^2 + \left( \dfrac{dy}{d\theta} \right)^2$

$\left( \dfrac{ds}{d\theta} \right)^2 = \left( \dfrac{dr}{d\theta} \cos \theta - r\sin \theta \right)^2 + \left( \dfrac{dr}{d\theta} \sin \theta + r\cos \theta \right)^2$

$\left( \dfrac{ds}{d\theta} \right)^2 = \left[ \left( \dfrac{dr}{d\theta} \right)^2 \cos^2 \theta - 2r \sin \theta \cos \theta \dfrac{dr}{d\theta} + r^2 \sin^2 \theta \right] \\ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ + \left[ \left( \dfrac{dr}{d\theta} \right)^2 \sin^2 \theta + 2r \sin \theta \cos \theta \dfrac{dr}{d\theta} + r^2 \cos^2 \theta \right]$

$\left( \dfrac{ds}{d\theta} \right)^2 = \left( \dfrac{dr}{d\theta} \right)^2 \cos^2 \theta + r^2 \sin^2 \theta + \left( \dfrac{dr}{d\theta} \right)^2 \sin^2 \theta + r^2 \cos^2 \theta$

$\left( \dfrac{ds}{d\theta} \right)^2 = \left( r^2 \sin^2 \theta + r^2 \cos^2 \theta \right) + \left[ \left( \dfrac{dr}{d\theta} \right)^2 \sin^2 \theta + \left( \dfrac{dr}{d\theta} \right)^2 \cos^2 \theta \right]$

$\left( \dfrac{ds}{d\theta} \right)^2 = r^2 \left( \sin^2 \theta + \cos^2 \theta \right) + \left( \dfrac{dr}{d\theta} \right)^2 \left( \sin^2 \theta + \cos^2 \theta \right)$

$\left( \dfrac{ds}{d\theta} \right)^2 = r^2 + \left( \dfrac{dr}{d\theta} \right)^2$

$\dfrac{ds}{d\theta} = \sqrt{r^2 + \left( \dfrac{dr}{d\theta} \right)^2}$

$ds = \sqrt{r^2 + \left( \dfrac{dr}{d\theta} \right)^2} ~ d\theta$
 

Integrate both sides:

Another way to derive the formula
ds_r = arc of a circle of radius r and central angle dθ
$\dfrac{ds_r}{d\theta} = \dfrac{2\pi r}{2\pi}$

$\dfrac{ds_r}{d\theta} = r$
 

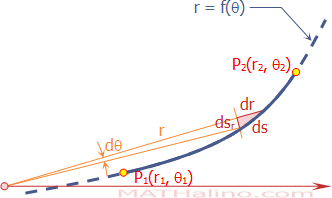
From the figure above:
$(ds)^2 = (ds_r)^2 + (dr)^2$

$\left( \dfrac{ds}{d\theta} \right)^2 = \left( \dfrac{ds_r}{d\theta} \right)^2 + \left( \dfrac{dr}{d\theta} \right)^2$

$\left( \dfrac{ds}{d\theta} \right)^2 = r^2 + \left( \dfrac{dr}{d\theta} \right)^2$

$\dfrac{ds}{d\theta} = \sqrt{r^2 + \left( \dfrac{dr}{d\theta} \right)^2}$

$ds = \sqrt{r^2 + \left( \dfrac{dr}{d\theta} \right)^2} \, d\theta$
 

Integrate both sides:
$\displaystyle s = \int_{\theta_1}^{\theta_2} \sqrt{r^2 + \left( \dfrac{dr}{d\theta} \right)^2} ~ d\theta$           okay!