For rectangular area
$A_1 = 90(60) = 5400 \, \text{ mm}^2$
$x_1 = \frac{1}{2}(90) = 45 \, \text{ mm}$
$y_1 = \frac{1}{2}(60) = 30 \, \text{ mm}$
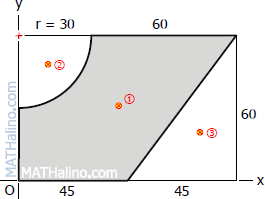For quarter circle
$A_2 = \frac{1}{4}\pi r^2 = \frac{1}{4}\pi (30^2) = 706.86 \, \text{ mm}^2$
$x_2 = \dfrac{4r}{3\pi} = \dfrac{4(30)r}{3\pi} = 12.73 \, \text{ mm}$
$y_2 = 60 - \dfrac{4r}{3\pi} = 60 - \dfrac{4(30)}{3\pi} = 47.27 \, \text{ mm}$
For the triangle
$A_3 = \frac{1}{2}(45)(60) = 1350 \, \text{ mm}^2$
$x_3 = 45 + \frac{2}{3}(45) = 75 \, \text{ mm}$
$y_3 = \frac{1}{3}(60) = 20 \, \text{ mm}$
For the shaded region
$A = A_1 - A_2 - A_3 = 5400 - 706.86 - 1350$
$A = 3343.14 \, \text{ mm}^2$
$A\bar{x} = \Sigma ax$
$3343.14\bar{x} = 5400(45) - 706.86(12.73) - 1350(75)$
$\bar{x} = 39.71 \, \text{ mm}$ answer
$A\bar{y} = \Sigma ay$
$3343.14\bar{y} = 5400(30) - 706.86(47.27) - 1350(20)$
$\bar{y} = 30.39 \, \text{ mm}$ answer
