Centroids and Centers of Gravity

Contents

  1. Centroids of Composite Figures
  2. Center of Gravity of Bodies and Centroids of Volumes
  3. Centroids Determined by Integration
Back to top

Centroids of Composite Figures

Center of gravity of a homogeneous flat plate
$W \, \bar{x} = \Sigma wx$

$W \, \bar{y} = \Sigma wy$

 

Centroids of areas
$A \, \bar{x} = \Sigma ax$

$A \, \bar{y} = \Sigma ay$

 

Centroids of lines
$L \, \bar{x} = \Sigma lx$

$L \, \bar{y} = \Sigma ly$

 

Back to top

Center of Gravity of Bodies and Centroids of Volumes

Center of gravity of bodies
$W \, \bar{x} = \Sigma wx$

$W \, \bar{y} = \Sigma wy$

$W \, \bar{z} = \Sigma wz$

 

Centroids of volumes
$V \, \bar{x} = \Sigma vx$

$V \, \bar{y} = \Sigma vy$

$V \, \bar{z} = \Sigma vz$

 

Back to top

Centroids Determined by Integration

Centroid of area
$\displaystyle A \, \bar{x} = \int_a^b x_c \, dA$

$\displaystyle A \, \bar{y} = \int_a^b y_c \, dA$

 

Centroid of lines
$\displaystyle L \, \bar{x} = \int_a^b x_c \, dL$

$\displaystyle L \, \bar{y} = \int_a^b y_c \, dL$

 

Center of gravity of bodies
$\displaystyle W \, \bar{x} = \int_a^b x_c \, dW$

$\displaystyle W \, \bar{y} = \int_a^b y_c \, dW$

$\displaystyle W \, \bar{z} = \int_a^b z_c \, dW$

 

Centroids of volumes
$\displaystyle V \, \bar{x} = \int_a^b x_c \, dV$

$\displaystyle V \, \bar{y} = \int_a^b y_c \, dV$

$\displaystyle V \, \bar{z} = \int_a^b z_c \, dV$

 

Centroids of Common Geometric Shapes

Rectangle Area and Centroid
 
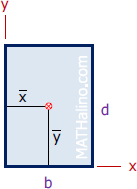centroid and area of rectangle
 		 $A = bd$

$\bar{x} = \frac{1}{2}b$

$\bar{y} = \frac{1}{2}d$

 

Triangle Area and Centroid
 
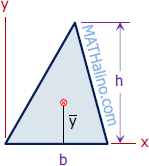centroid and area of triangle
 		 $A = \frac{1}{2}bh$

$\bar{y} = \frac{1}{3}h$

 

Circle Area and Centroid
 
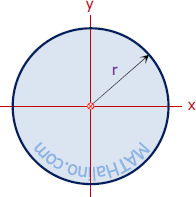000-circle.gif
 		 $A = \pi r^2$

$\bar{x} = 0$

$\bar{y} = 0$

 

Semicircle Area and Centroid
 
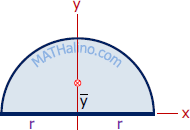centroid and area of semicircle
 		 $A = \frac{1}{2}\pi r^2$

$\bar{x} = 0$

$\bar{y} = \dfrac{4r}{3\pi}$

 

Semicircular Arc Length and Centroid
 
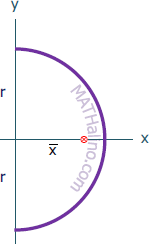centroid and length of semicircular arc
 		 $L = \pi r$

$\bar{x} = \dfrac{2r}{\pi}$

$\bar{y} = 0$

 

Quarter Circle Area and Centroid
 
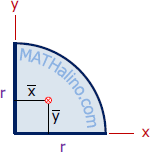centroid and area of quarter circle.gif
 		 $A = \frac{1}{4}\pi r^2$

$\bar{x} = \dfrac{4r}{3\pi}$

$\bar{y} = \dfrac{4r}{3\pi}$

 

Sector of a Circle Area and Centroid
 
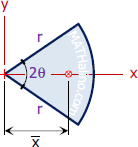centroid and area of circular sector
 		 $A = r^2 \theta_{rad}$

$\bar{x} = \dfrac{2r \sin \theta}{3\theta_{rad}}$

$\bar{y} = 0$

 

Circular Arc Length and Centroid
 
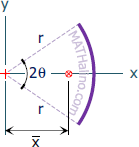centroid and length of circular arc
 		 $L = 2r \theta_{rad}$

$\bar{x} = \dfrac{r \sin \theta}{\theta_{rad}}$

$\bar{y} = 0$

 

Ellipse Area and Centroid
 
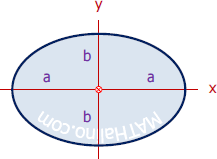centroid and area of ellipse
 		 $A = \pi ab$

$\bar{x} = 0$

$\bar{y} = 0$

 

Half Ellipse Area and Centroid
 
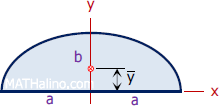centroid and area of half ellipse
 		 $A = \frac{1}{2}\pi ab$

$\bar{x} = 0$

$\bar{y} = \dfrac{4b}{3\pi}$

 

Quarter Ellipse Area and Centroid
 
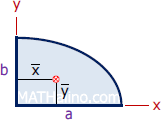centroid and area of quarter ellipse
 		 $A = \frac{1}{4}\pi ab$

$\bar{x} = \dfrac{4a}{3\pi}$

$\bar{y} = \dfrac{4b}{3\pi}$

 

Parabolic Segment Area and Centroid
 
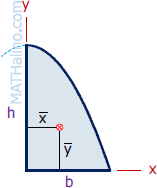centroid and area of parabolic segment
 		 $A = \frac{2}{3} bh$

$\bar{x} = \frac{3}{8}b$

$\bar{y} = \frac{2}{5}h$

 

Spandrel Area and Centroid
 
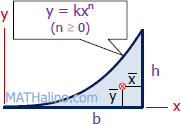000-spandrel.gif
 		 $A = \dfrac{1}{n + 1} bh$

$\bar{x} = \dfrac{1}{n + 2}b$

$\bar{y} = \dfrac{n + 1}{4n + 2}h$

 

Back to top
Tags
centroid
center of gravity
centroid by integration
centroid of area
centroid of line
centroid of common areas
centroid of volume