Shear and Moment in Beams
Definition of a Beam
A beam is a bar subject to forces or couples that lie in a plane containing the longitudinal section of the bar. According to determinacy, a beam may be determinate or indeterminate.
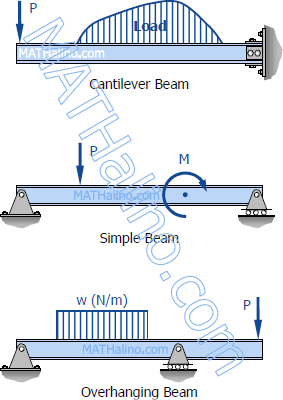
Statically Determinate Beams
Statically determinate beams are those beams in which the reactions of the supports may be determined by the use of the equations of static equilibrium. The beams shown below are examples of statically determinate beams.
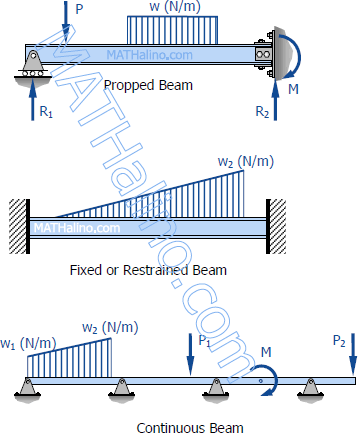
Statically Indeterminate Beams
If the number of reactions exerted upon a beam exceeds the number of equations in static equilibrium, the beam is said to be statically indeterminate. In order to solve the reactions of the beam, the static equations must be supplemented by equations based upon the elastic deformations of the beam.
The degree of indeterminacy is taken as the difference between the umber of reactions to the number of equations in static equilibrium that can be applied. In the case of the propped beam shown, there are three reactions R1, R2, and M and only two equations (ΣM = 0 and ΣFv = 0) can be applied, thus the beam is indeterminate to the first degree (3 - 2 = 1).
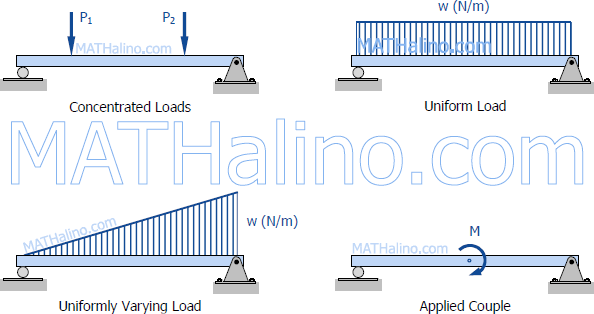
Types of Loading
Loads applied to the beam may consist of a concentrated load (load applied at a point), uniform load, uniformly varying load, or an applied couple or moment. These loads are shown in the following figures.