Relationship Between Load, Shear, and Moment

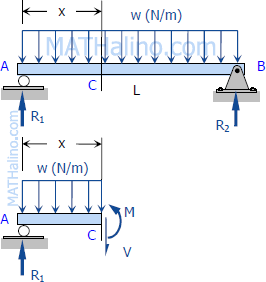The vertical shear at C in the figure shown in previous section (also shown to the right) is taken as
$V_C = (\Sigma F_v)_L = R_1 - wx$
 

where R₁ = R₂ = wL/2
 

$V_c = \dfrac{wL}{2} - wx$
 

The moment at C is
$M_C = (\Sigma M_C) = \dfrac{wL}{2}x - wx \left( \dfrac{x}{2} \right)$

$M_C = \dfrac{wLx}{2} - \dfrac{wx^2}{2}$
 

If we differentiate M with respect to x:
$\dfrac{dM}{dx} = \dfrac{wL}{2} \cdot \dfrac{dx}{dx} - \dfrac{w}{2} \left( 2x \cdot \dfrac{dx}{dx} \right)$

$\dfrac{dM}{dx} = \dfrac{wL}{2} - wx = \text{shear}$
 

thus,

Thus, the rate of change of the bending moment with respect to x is equal to the shearing force, or the slope of the moment diagram at the given point is the shear at that point.
 

Differentiate V with respect to x gives
$\dfrac{dV}{dx} = 0 - w$
 

thus,

Thus, the rate of change of the shearing force with respect to x is equal to the load or the slope of the shear diagram at a given point equals the load at that point.
 

Properties of Shear and Moment Diagrams
The following are some important properties of shear and moment diagrams:

1. The area of the shear diagram to the left or to the right of the section is equal to the moment at that section.
2. The slope of the moment diagram at a given point is the shear at that point.
3. The slope of the shear diagram at a given point equals the load at that point.



4. The maximum moment occurs at the point of zero shears. This is in reference to property number 2, that when the shear (also the slope of the moment diagram) is zero, the tangent drawn to the moment diagram is horizontal.
5. When the shear diagram is increasing, the moment diagram is concave upward.
6. When the shear diagram is decreasing, the moment diagram is concave downward.

Sign Convention
The customary sign conventions for shearing force and bending moment are represented by the figures below. A force that tends to bend the beam downward is said to produce a positive bending moment. A force that tends to shear the left portion of the beam upward with respect to the right portion is said to produce a positive shearing force.
 

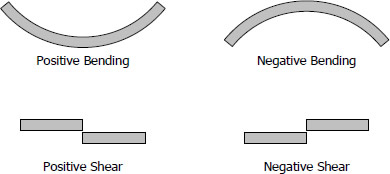
An easier way of determining the sign of the bending moment at any section is that upward forces always cause positive bending moments regardless of whether they act to the left or to the right of the exploratory section.
 

INSTRUCTION:
Without writing shear and moment equations, draw the shear and moment diagrams for the beams specified in the following problems. Give numerical values at all change of loading positions and at all points of zero shear. (Note to instructor: Problems 403 to 420 may also be assigned for solution by semi-graphical method describes in this article.)