Properties of Triangle

Side
Side of a triangle is a line segment that connects two vertices. Triangle has three sides, it is denoted by a, b, and c in the figure below.

Vertex
Vertex is the point of intersection of two sides of triangle. The three vertices of the triangle are denoted by A, B, and C in the figure below. Notice that the opposite of vertex A is side a, opposite to vertex B is side B, and opposite to vertex C is side c.

Included Angle or Vertex Angle
Included angle is the angle subtended by two sides at the vertex of the triangle. It is also called vertex angle. For convenience, each included angle has the same notation to that of the vertex, ie. angle A is the included angle at vertex A, and so on. The sum of the included angles of the triangle is always equal to 180°.

$A + B + C = 180^\circ$

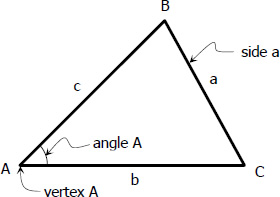
Side, vertex, and included angle of a triangle

Altitude, h
Altitude is a line from vertex perpendicular to the opposite side. The altitudes of the triangle will intersect at a common point called orthocenter.

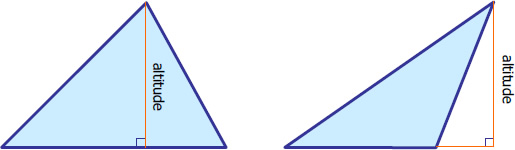
If sides a, b, and c are known, solve one of the angles using Cosine Law then solve the altitude of the triangle by functions of a right triangle. If the area of the triangle A_t is known, the following formulas are useful in solving for the altitudes.

$h_A = \dfrac{2A_t}{a}; \,\, h_B = \dfrac{2A_t}{b}; \,\, h_C = \dfrac{2A_t}{c}$

Base
The base of the triangle is relative to which altitude is being considered. Figure below shows the bases of the triangle and its corresponding altitude.

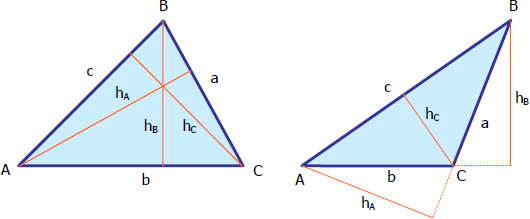
If h_A is taken as altitude then side a is the base
If h_B is taken as altitude then side b is the base
If h_C is taken as altitude then side c is the base

Median, m
Median of the triangle is a line from vertex to the midpoint of the opposite side. A triangle has three medians, and these three will intersect at the centroid. The figure below shows the median through A denoted by m_A.

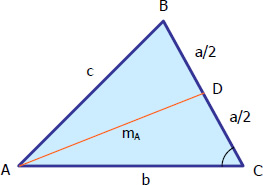
Given three sides of the triangle, the median can be solved by two steps.

Solve for one included angle, say angle C, using Cosine Law. From the figure above, solve for C in triangle ABC.
Using triangle ADC, determine the median through A by Cosine Law.

The formulas below, though not recommended, can be used to solve for the length of the medians.

$4{m_A}^2 = 2b^2 + 2c^2 - a^2$

$4{m_B}^2 = 2a^2 + 2c^2 - b^2$

$4{m_C}^2 = 2a^2 + 2b^2 - c^2$

Where m_A, m_B, and m_C are medians through A, B, and C, respectively.

Angle Bisector
Angle bisector of a triangle is a line that divides one included angle into two equal angles. It is drawn from vertex to the opposite side of the triangle. Since there are three included angles of the triangle, there are also three angle bisectors, and these three will intersect at the incenter. The figure shown below is the bisector of angle A, its length from vertex A to side a is denoted as b_A.

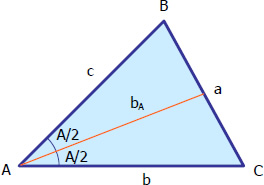
The length of angle bisectors is given by the following formulas:

$b_A = \dfrac{2\sqrt{bcs\,(s - a)}}{b + c}$

$b_B = \dfrac{2\sqrt{acs\,(s - b)}}{a + c}$

$b_C = \dfrac{2\sqrt{abs\,(s - c)}}{a + b}$

where $s = \frac{1}{2}(a + b + c)$ called the semi-perimeter and b_A, b_B, and b_C are bisectors of angles A, B, and C, respectively. The given formulas are not worth memorizing for if you are given three sides, you can easily solve the length of angle bisectors by using the Cosine and Sine Laws.

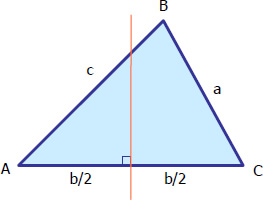
Perpendicular Bisector
Perpendicular bisector of the triangle is a perpendicular line that crosses through midpoint of the side of the triangle. The three perpendicular bisectors are worth noting for it intersects at the center of the circumscribing circle of the triangle. The point of intersection is called the circumcenter. The figure below shows the perpendicular bisector through side b.

Navigation

Recent comments