Derivation of Formula for Volume of the Sphere by Integration

For detailed information about sphere, see the Solid Geometry entry, The Sphere.
 

The formula for the volume of the sphere is given by

Where, r = radius of the sphere
 

Derivation for Volume of the Sphere
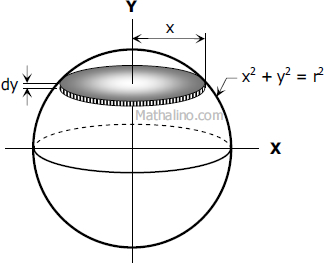The differential element shown in the figure is cylindrical with radius x and altitude dy. The volume of cylindrical element is...
$dV = \pi x^2 dy$
 

The sum of the cylindrical elements from 0 to r is a hemisphere, twice the hemisphere will give the volume of the sphere. Thus,
$\displaystyle V = 2\pi \int_0^r x^2 dy$

 
From the equation of the circle x² + y² = r²; x² = r² - y².

$\displaystyle V = 2\pi \int_0^r (r^2 - y^2) dy$

$V = 2\pi \left[ r^2y - \dfrac{y^3}{3} \right]_0^r$

$V = 2\pi \left[ \left(r^3 - \dfrac{r^3}{3}\right) - \left(0 - \dfrac{0^3}{3}\right) \right]$

$V = 2\pi \left[ \dfrac{2r^3}{3} \right]$

$V = \dfrac{4 \pi r^3}{3}$       okay!