Derivation / Proof of Ptolemy's Theorem for Cyclic Quadrilateral

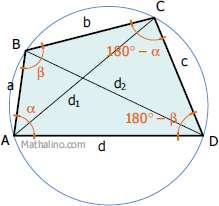
Ptolemy's theorem for cyclic quadrilateral states that the product of the diagonals is equal to the sum of the products of opposite sides. From the figure below, Ptolemy's theorem can be written as
 

 

Proof of Ptolemy's Theorem
Note that the diagonal d₁ is from A to C and diagonal d₂ is from B to D. If you have question why the angle at vertex C is (180° - α) and (180° - β) at vertex D, see the page of Cyclic Quadrilateral.
 

 

Cosine law for triangle ABC
${d_1}^2 = a^2 + b^2 – 2ab \cos \beta$   → equation (1)
 

Cosine law for triangle ADC
${d_1}^2 = c^2 + d^2 – 2cd \cos (180^\circ – \beta)$

${d_1}^2 = c^2 + d^2 + 2cd \cos \beta$   → equation (2)
 

Equate equations (1) and (2)
${d_1}^2 = {d_1}^2$

$a^2 + b^2 – 2ab \cos \beta = c^2 + d^2 + 2cd \cos \beta$

$a^2 + b^2 – c^2 - d^2 = 2ab \cos \beta + 2cd \cos \beta$

$a^2 + b^2 – c^2 - d^2 = 2(ab + cd) \cos \beta$

$\cos \beta = \dfrac{a^2 + b^2 – c^2 - d^2}{2(ab + cd)}$
 

Substitute the value of cos β to equation (1)
${d_1}^2 = a^2 + b^2 – 2ab \left[ \dfrac{a^2 + b^2 – c^2 - d^2}{2(ab + cd)} \right]$

${d_1}^2 = a^2 + b^2 – \dfrac{a^3b + ab^3 – abc^2 - abd^2}{ab + cd}$

${d_1}^2 = \dfrac{(a^2 + b^2)(ab + cd) - (a^3b + ab^3 – abc^2 - abd^2)}{ab + cd}$

${d_1}^2 = \dfrac{a^3b + a^2cd + ab^3 + b^2cd - a^3b - ab^3 + abc^2 + abd^2}{ab + cd}$

${d_1}^2 = \dfrac{a^2cd + b^2cd + abc^2 + abd^2}{ab + cd}$

${d_1}^2 = \dfrac{(a^2cd + abc^2) + (abd^2 + b^2cd)}{ab + cd}$

${d_1}^2 = \dfrac{ac(ad + bc) + bd(ad + bc)}{ab + cd}$

${d_1}^2 = \dfrac{(ac + bd)(ad + bc)}{ab + cd}$   → equation (3)
 

In the same manner, find the value of d₂². Cosine law for triangle BAD
${d_2}^2 = a^2 + d^2 – 2ad \cos \alpha$   → equation (4)
 

Cosine law for triangle BCD
${d_2}^2 = b^2 + c^2 – 2bc \cos (180^\circ – \alpha)$

${d_2}^2 = b^2 + c^2 + 2bc \cos \alpha$   → equation (5)
 

Equate equations (4) and (5)
${d_2}^2 = {d_2}^2$

$a^2 + d^2 – 2ad \cos \alpha = b^2 + c^2 + 2bc \cos \alpha$

$a^2 + d^2 – b^2 - c^2 = 2ad \cos \alpha + 2bc \cos \alpha$

$a^2 + d^2 – b^2 - c^2 = 2(ad + bc) \cos \alpha$

$\cos \alpha = \dfrac{a^2 + d^2 – b^2 - c^2}{2(ad + bc)}$
 

Substitute the value of cos α to equation (4)
${d_2}^2 = a^2 + d^2 – 2ad \left[ \dfrac{a^2 + d^2 – b^2 - c^2}{2(ad + bc)} \right]$

${d_2}^2 = a^2 + d^2 – \dfrac{a^3d + ad^3 – ab^2d - ac^2d}{ad + bc}$

${d_2}^2 = \dfrac{(a^2 + d^2)(ad + bc) - (a^3d + ad^3 – ab^2d - ac^2d)}{ad + bc}$

${d_2}^2 = \dfrac{a^3d + a^2bc + ad^3 + bcd^2 - a^3d - ad^3 + ab^2d + ac^2d}{ad + bc}$

${d_2}^2 = \dfrac{a^2bc + bcd^2 + ab^2d + ac^2d}{ad + bc}$

${d_2}^2 = \dfrac{(a^2bc + ab^2d) + (ac^2d + bcd^2)}{ad + bc}$

${d_2}^2 = \dfrac{ab(ac + bd) + cd(ac + bd)}{ad + bc}$

${d_2}^2 = \dfrac{(ab + cd)(ac + bd)}{ad + bc}$   → equation (6)
 

Multiply equation (3) and equation (6)
${d_1}^2 \times {d_2}^2 = \dfrac{(ac + bd)(ad + bc)}{ab + cd} \times \dfrac{(ab + cd)(ac + bd)}{ad + bc}$

$(d_1 d_2)^2 = (ac + bd)^2$
 

Thus,