Stability of Floating Bodies

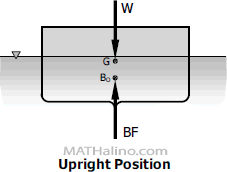
Any floating body is subjected by two opposing vertical forces. One is the body's weight W which is downward, and the other is the buoyant force BF which is upward. The weight is acting at the center of gravity G and the buoyant force is acting at the center of buoyancy BO. W and BF are always equal and if these forces are collinear, the body will be in upright position as shown below.
 

The body may tilt from many causes like wind or wave action causing the center of buoyancy to shift to a new position B_O' as shown below.
 

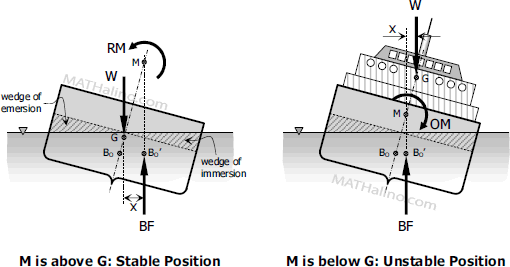
Point M is the intersection of the axis of the body and the line of action of the buoyant force, it is called metacenter. If M is above G, BF and W will produce a righting moment RM which causes the body to return to its neutral position, thus the body is stable. If M is below G, the body becomes unstable because of the overturning moment OM made by W and BF. If M coincides with G, the body is said to be just stable which simply means critical. The value of righting moment or overturning moment is given by
 

The distance MG is called metacentric height.
 

Use (-) if G is above B_O and (+) if G is below B_O. Note that M is always above B_O.
 

Value of MB_O
Assume that the body is rectangular at the top view and measures B by L at the waterline when in upright position. The moment due to the shifting of the buoyant force is equal to the moment due to shifting of wedge.
 

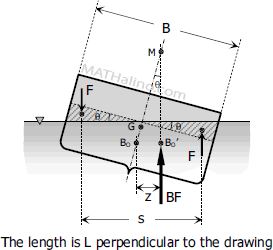
$BF \, z = Fs$

$\gamma V_D \, (MB_O \sin \theta) = (\gamma v)s$

$V_D MB_O \sin \theta = vs$

$MB_O = \dfrac{[ \, \frac{1}{2}(\frac{1}{2}B)(\frac{1}{2}B \tan \theta)L \,](\frac{2}{3}B)}{V_D \sin \theta}$

$MB_O = \dfrac{\frac{1}{12}LB^3 \tan \theta}{V_D \sin \theta}$
 

For small value of θ, tan θ ≡ sin θ and note that 1/12 LB³ = I, thus,

$MB_O = \dfrac{I \sin \theta}{V_D \sin \theta}$

The formula above can be applied to any section.
 

Where
W = weight of the body
BF = buoyant force
M = metacenter
G = center of gravity of the body
B_O = center of buoyancy in upright position
B_O' = center of buoyancy in tilted position
MG = metacentric height or the distance from M to G
MB_O = distance from M to B_O
G_O = distance from G to B_O
v = volume of the wedge either immersion or emersion
s = horizontal distance between the center of gravity of the wedges
θ = angle of tilting
I = moment of inertia of the waterline section of the body
RM = righting moment
OM = overturning moment
 

For rectangular section