Method of Superposition | Beam Deflection

The slope or deflection at any point on the beam is equal to the resultant of the slopes or deflections at that point caused by each of the load acting separately.
 

Rotation and Deflection for Common Loadings

Case 1: Concentrated load at the free end of cantilever beam
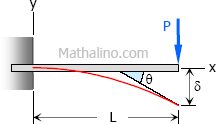Maximum Moment
$M = -PL$

Slope at end
$\theta = \dfrac{PL^2}{2EI}$

Maximum deflection
$\delta = \dfrac{PL^3}{3EI}$

Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac{Px^2}{6}(3L - x)$
 

Case 2: Concentrated load at any point on the span of cantilever beam
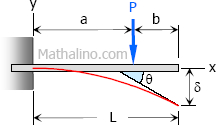Maximum Moment
$M = -Pa$

Slope at end
$\theta = \dfrac{Pa^2}{2EI}$

Maximum deflection
$\delta = \dfrac{Pa^2}{6EI}(3L - a)$

Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac{Px^2}{6}(3a - x) \text{ for } 0 \lt x \lt a$

$EI \, y = \dfrac{Pa^2}{6}(3x - a) \text{ for } a \lt x \lt L$
 

Case 3: Uniformly distributed load over the entire length of cantilever beam
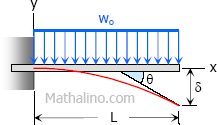Maximum Moment
$M = -\dfrac{w_oL^2}{2}$

Slope at end
$\theta = \dfrac{w_oL^3}{6EI}$

Maximum deflection
$\delta = \dfrac{w_oL^4}{8EI}$

Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac{w_ox^2}{24}(6L^2 - 4Lx + x^2)$
 

Case 4: Triangular load, full at the fixed end and zero at the free end, of cantilever beam
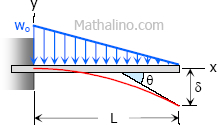Maximum Moment
$M = -\dfrac{w_oL^2}{6}$

Slope at end
$\theta = \dfrac{w_oL^3}{24EI}$

Maximum deflection
$\delta = \dfrac{w_oL^4}{30EI}$

Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac{w_ox^2}{120L}(10L^3 - 10L^2x + 5Lx^2 - x^3)$
 

Case 5: Moment load at the free end of cantilever beam
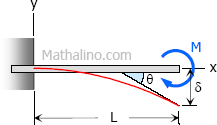Maximum Moment
$M = -M$

Slope at end
$\theta = \dfrac{ML}{EI}$

Maximum deflection
$\delta = \dfrac{ML^2}{2EI}$

Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac{Mx^2}{2}$
 

Case 6: Concentrated load at the midspan of simple beam
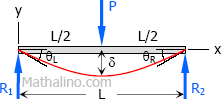Maximum Moment
$M = \dfrac{PL}{4}$

Slope at end
$\theta_L = \theta_R = \dfrac{PL^2}{16EI}$

Maximum deflection
$\delta = \dfrac{PL^3}{48EI}$

Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac{Px}{12}(\frac{3}{4}L^2 - x^2) \text{ for } 0 \lt x \lt \frac{1}{2}L$
 

Case 7: Concentrated load at any point on simple beam
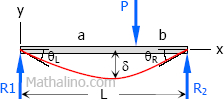Maximum Moment
$M = \dfrac{Pab}{L} \text{ at } x = a$

Slope at end
$\theta_L = \dfrac{Pb(L^2 - b^2)}{6EIL}$

$\theta_R = \dfrac{Pa(L^2 - a^2)}{6EIL}$

Maximum deflection
$\delta = \dfrac{Pb(L^2 - b^2)^{3/2}}{9\sqrt{3} \, EIL} \text{ at } x = \sqrt{\dfrac{L^2 - b^2}{3}}$

Deflection at the center (not maximum)
$\delta = \dfrac{Pb}{48EI}(3L^2 - 4b^2) \text{ when } a \gt b$

Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac{Pbx}{6L}(L^2 - x^2 - b^2) \text{ for } 0 \lt x \lt a$

$EI \, y = \dfrac{Pb}{6L} \left[ \dfrac{L}{b}(x - a)^3 + (L^2 - b^2)x - x^3 \right] \text{ for } a \lt x \lt L$
 

Case 8: Uniformly distributed load over the entire span of simple beam
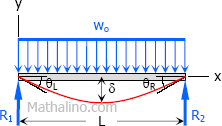Maximum Moment
$M = \dfrac{w_oL^2}{8}$

Slope at end
$\theta_L = \theta_R = \dfrac{w_oL^3}{24EI}$

Maximum deflection
$\delta = \dfrac{5w_oL^4}{384EI}$

Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac{w_ox}{24}(L^3 - 2Lx^2 + x^3)$
 

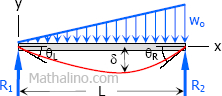
Case 9: Triangle load with zero at one support and full at the other support of simple beam
Maximum Moment
$M = \dfrac{w_oL^2}{9\sqrt{3}}$

Slope at end
$\theta_L = \dfrac{7w_oL^3}{360EI}$

$\theta_R = \dfrac{8w_oL^3}{360EI}$

Maximum deflection
$\delta = \dfrac{2.5w_oL^4}{384EI} \text{ at } x = 0.519L$

Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac{w_ox}{360L}(7L^4 - 10L^2x^2 + 3x^4)$
 

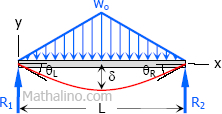
Case 10: Triangular load with zero at each support and full at the midspan of simple beam
Maximum Moment
$M = \dfrac{w_oL^2}{12}$

Slope at end
$\theta_L = \theta_R = \dfrac{5w_oL^3}{192EI}$

Maximum deflection
$\delta = \dfrac{w_oL^4}{120EI}$

Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac{w_ox}{960L}(25L^4 - 40L^2x^2 + 16x^4) \text{ for } 0 \lt x \lt \dfrac{L}{2}$
 

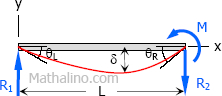
Case 11: Moment load at the right support of simple beam
Maximum Moment
$M = M$

Slope at end
$\theta_L = \dfrac{ML}{6EI}$

$\theta_R = \dfrac{ML}{3EI}$

Maximum deflection
$\delta = \dfrac{ML^2}{9\sqrt{3} \, EI} \text{ at } x = \dfrac{L}{\sqrt{3}}$

Deflection at the center (not maximum)
$\delta = \dfrac{ML^2}{16EI}$

Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac{MLx}{6}\left( 1 - \dfrac{x^2}{L^2} \right)$
 

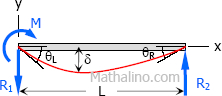
Case 12: Moment load at the left support of simple beam
Maximum Moment
$M = M$

Slope at end
$\theta_L = \dfrac{ML}{3EI}$

$\theta_R = \dfrac{ML}{6EI}$

Maximum deflection
$\delta = \dfrac{ML^2}{9\sqrt{3} \, EI} \text{ at } x = \left( L - \dfrac{L}{\sqrt{3}} \right)$

Deflection at the center (not maximum)
$\delta = \dfrac{ML^2}{16EI}$

Deflection Equation ($y$ is positive downward)
$EI \, y = \dfrac{Mx}{6L}(L - x)(2L - x)$