Components of a Force

Tags:

Forces acting at some angle from the the coordinate axes can be resolved into mutually perpendicular forces called components. The component of a force parallel to the x-axis is called the x-component, parallel to y-axis the y-component, and so on.

Components of a Force in XY Plane
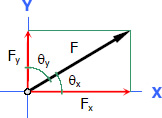
$F_x = F \cos \theta_x = F \sin \theta_y$

$F_y = F \sin \theta_x = F \cos \theta_y$

$F= \sqrt{{F_x}^2 + {F_y}^2}$

$\tan \theta_x = \dfrac{F_y}{F_x}$

Given the slope of the line of action of the force as v/h (see figure to the right)
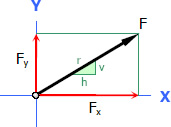
$r =\sqrt{h^2 + v^2}$

$F_x = F (h/r)$

$F_y = F (v/r)$

Components of a Force in 3D Space
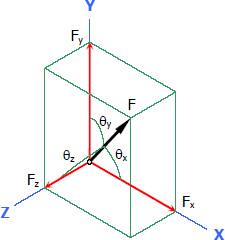
Given the direction cosines of the force:
$F_x = F \cos \theta_x$

$F_y = F \cos \theta_y$

$F_z = F \cos \theta_z$

$F = \sqrt{{F_x}^2 + {F_y}^2 + {F_z}^2}$

$\cos \theta_x = \dfrac{F_x}{F}$

$\cos \theta_y = \dfrac{F_y}{F}$

$\cos \theta_z = \dfrac{F_z}{F}$

Components of a force in 3D space Given the coordinates of any two points along the line of action of the force (in reference to the figure shown, one of the points is the origin):
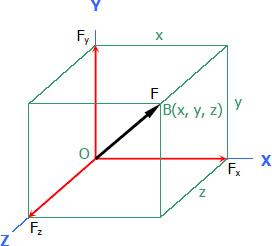
Let d = distance OB
$d = \sqrt{x^2 + y^2 + z^2}$

$F_x = F (x/d)$

$F_y = F (y/d)$

$F_z = F (z/d)$

Vector Notation of a Force (Also called Rectangular Representation of a Force)

${\bf F} = F{\bf \lambda}$

Where λ is a unit vector. There are two cases in determining λ; by direction cosines and by the coordinates of any two points on the line of action of the force.

Given the direction cosines:
${\bf \lambda} = \cos \theta_x {\bf i} + \cos \theta_y {\bf j} + \cos \theta_z {\bf k}$

Given any two points P₁(x₁, y₁) and P₂(x₂, y₂) on the line of action of the force:
${\bf \lambda} = \dfrac{1}{d} \left( d_x{\bf i} + d_y {\bf j} + d_z {\bf k} \right)$