Resultant of Parallel Force System
Coplanar Parallel Force System
Parallel forces can be in the same or in opposite directions. The sign of the direction can be chosen arbitrarily, meaning, taking one direction as positive makes the opposite direction negative. The complete definition of the resultant is according to its magnitude, direction, and line of action.
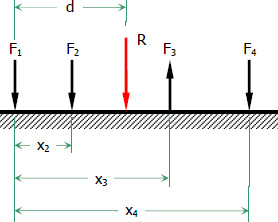
$Rd = \Sigma Fx = F_1 x_1 + F_2 x_2 + F_3 x_3 + ...$
Resultant of Distributed Loads
The resultant of a distributed load is equal to the area of the load diagram. It is acting at the centroid of that area as indicated. The figure below shows the three common distributed loads namely; rectangular load, triangular load, and trapezoidal load.
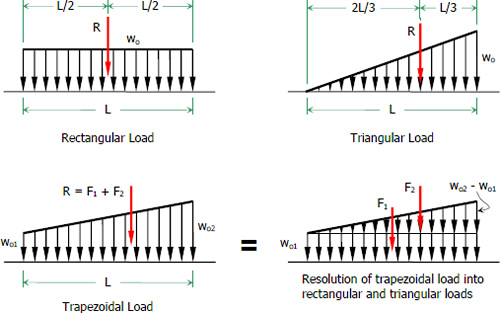
$R = w_o L$
Triangular Load
$R = \frac{1}{2}w_o L$
Trapezoidal Load
$R = w_{o1} L + \frac{1}{2}(w_{o2} - w_{o1}) L$
Spatial Parallel Force System
The resultant of parallel forces in space will act at the point where it will create equivalent translational and rotational (moment) effects in the system.
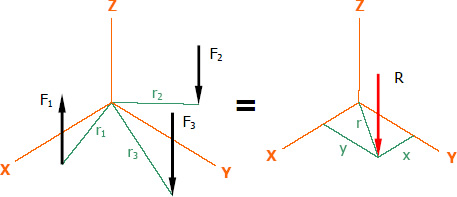
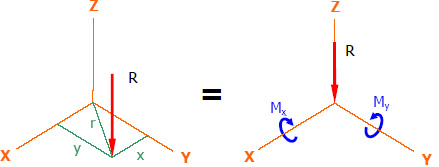
In vector notation, the resultant of forces are as follows...
$\bf {M_o} = \bf {r_1} \times \bf {F_1} \, + \, \bf {r_2} \times \bf {F_2} \, + \, \bf {r_3} \times \bf {F_3} \, + \, ...$
Note:
Two parallel forces that are equal in magnitude, opposite in direction, and not colinear will create a rotation effect. This type of pair is called a Couple. The placement of a couple in the plane is immaterial, meaning, its rotational effect to the body is not a function of its placement. The magnitude of the couple is given by
Where F = the magnitude of the two equal opposing forces and d is the perpendicular distance between these forces.
- Log in to post comments
