Part a: Unknown force and direction with non-zero resultant
$R_x = 0$ and $R_y = 300 \, \text{ N}$
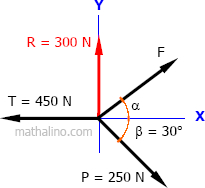$R_x = \Sigma F_x$
$0 = F \cos \alpha + 250 \cos 30^\circ - 450$
$F \cos \alpha = 233.49$
$F = \dfrac{233.49}{\cos \alpha}$
$R_y = \Sigma F_y$
$300 = F \sin \alpha - 250 \sin 30^\circ$
$F \sin \alpha = 425$
$\left( \dfrac{233.49}{\cos \alpha} \right) \sin \alpha = 425$
$\tan \alpha = 1.8202$
$\alpha = 61.22^\circ$ answer
$F = \dfrac{233.49}{\cos 61.22^\circ}$
$F = 484.92 \, \text{ N}$ answer
Part b: Unknown force and direction with zero resultant
$R_x = 0$ and $R_y = 0$
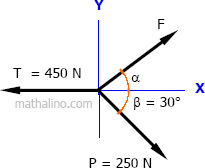$R_x = \Sigma F_x$
$0 = F \cos \alpha + 250 \cos 30^\circ - 450$
$F \cos \alpha = 233.49$
$F = \dfrac{233.49}{\cos \alpha}$
$R_y = \Sigma F_y$
$0 = F \sin \alpha - 250 \sin 30^\circ$
$F \sin \alpha = 125$
$\left( \dfrac{233.49}{\cos \alpha} \right)\sin \alpha = 125$
$\tan \alpha = 0.5354$
$\alpha = 28.16^\circ$ answer
$F = \dfrac{233.49}{\cos 28.16^\circ}$
$F = 264.85 \, \text{ N}$ answer
Part c: Unknown direction of two forces with zero resultant
$R_x = 0$ and $R_y = 0$
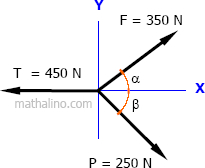$R_y = \Sigma F_y$
$0 = 350 \sin \alpha - 250 \sin \beta$
$7 \sin \alpha - 5 \sin \alpha = 0$
$7 \sin \alpha = 5 \sin \beta$
$49 \sin^2 \alpha = 25 \sin^2 \beta$ → Equation (1)
$R_x = \Sigma F_x$
$0 = 350 \cos \alpha + 250 \cos \beta - 450$
$7 \cos \alpha + 5 \cos \beta - 9 = 0$
$7 \cos \alpha = 9 - 5 \cos \alpha$
$49 \cos^2 \alpha = (9 - 5 \cos \alpha)^2$
$49 \cos^2 \alpha = 81 - 90 \cos \beta + 25 \cos^2 \beta$ → Equation (2)
Equation (1) + Equation (2)
$49 \sin^2 \alpha + 49 \cos^2 \alpha = 25 \sin^2 \beta + (81 - 90 \cos \beta + 25 \cos^2 \beta)$
$49(\sin^2 \alpha + \cos^2 \alpha) = 25(\sin^2 \beta + \cos^2 \beta) + 81 - 90 \cos \beta$
$49(1) = 25(1) + 81 - 90 \cos \beta$
$90 \cos \beta = 25 + 81 - 49$
$\cos \beta = \frac{57}{90}$
$\beta = 50.70^\circ$ answer
From Equation (1)
$49 \sin^2 \alpha = 25 \sin^2 50.70^\circ$
$7 \sin \alpha = 5 \sin 50.70^\circ$
$\sin \alpha = \frac{5}{7} \sin 50.70^\circ$
$\alpha = 33.56^\circ$ answer
Another Solution for Part c
