Axial Deformation

In the linear portion of the stress-strain diagram, the tress is proportional to strain and is given by
 

since $\sigma = P / A$ and $\varepsilon = \delta / L$, then $\dfrac{P}{A} = E \dfrac{\delta}{L}$
 

To use this formula, the load must be axial, the bar must have a uniform cross-sectional area, and the stress must not exceed the proportional limit.
 

If however, the cross-sectional area is not uniform, the axial deformation can be determined by considering a differential length and applying integration.
 

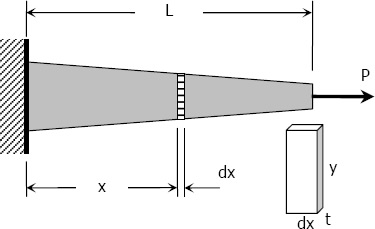
where A = ty, and y and t if variable, must be expressed in terms of x.
 

For a rod of unit mass ρ suspended vertically from one end, the total elongation due to its own weight is
 

where ρ is in kg/m³, L is the length of the rod in mm, M is the total mass of the rod in kg, A is the cross-sectional area of the rod in mm², and g = 9.81 m/s₂.
 

Stiffness, k
Stiffness is the ratio of the steady force acting on an elastic body to the resulting displacement. It has the unit of N/mm.