Thermal Stress
Temperature changes cause the body to expand or contract. The amount δT, is given by
where α is the coefficient of thermal expansion in m/m°C, L is the length in meter, Ti and Tf are the initial and final temperatures, respectively in °C. For steel, α = 11.25 × 10-6 m/m°C.
If temperature deformation is permitted to occur freely, no load or stress will be induced in the structure. In some cases where temperature deformation is not permitted, an internal stress is created. The internal stress created is termed as thermal stress.
For a homogeneous rod mounted between unyielding supports as shown, the thermal stress is computed as:

deformation due to temperature changes;
deformation due to equivalent axial stress;
$\delta_P = \dfrac{PL}{AE} = \dfrac{\sigma L}{E}$
$\delta_T = \delta_P$
$\alpha L \, \Delta T = \dfrac{\sigma L}{E}$
where σ is the thermal stress in MPa, E is the modulus of elasticity of the rod in MPa.
If the wall yields a distance of x as shown, the following calculations will be made:
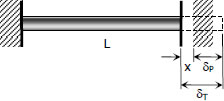
$\delta_T = x + \delta_P$
where σ represents the thermal stress.
Take note that as the temperature rises above the normal, the rod will be in compression, and if the temperature drops below the normal, the rod is in tension.
- Log in to post comments
