Horizontal Shearing Stress

Let us consider a differential length dx of the beam shown

In this section, f_v will be used for shearing
stress instead of the standard symbol τ.

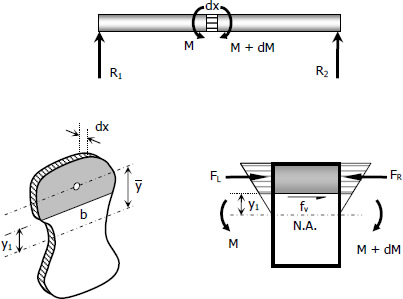
For the upper shaded portion of the beam, the forces acting are the total normal forces F_R and F_L due to the bending stresses to the left and to the right of the beam. These forces will be resisted by the shearing force f_vb dx acting at the boundary surface between the shaded and the unshaded portions.

For equilibrium of the upper shaded portion
$F_L + F_V - F_R = 0$

$F_V = F_R - F_L$

Where
$F_V = f_v b \, dx$

$\displaystyle F_L = \int f_{b1} \, dA ; \,\, f_{b1} = \frac{My}{I}$

$\displaystyle F_R = \int f_{b2} \, dA ; \,\, f_{b2} = \frac{(M + dM)y}{I}$

$\displaystyle F_v = \int \frac{(M + dM)y}{I} dA - \int \frac{My}{I} dA$

$\displaystyle f_v b \, dx = \int \frac{My}{I} dA + \int \frac{dM}{I} y \, dA - \int \frac{My}{I}$

$\displaystyle f_v b \, dx = \frac{dM}{I} \int y \, dA$

$\displaystyle f_v = \frac{1}{Ib} \frac{dM}{dx} \int y \, dA$

But $\,\, \dfrac{dM}{dx} = V, \,\,$ where $\,\, V \,\,$ represents the shear at the section in $\,\, N \,\,$ , and $\,\, \int y \, dA = A \bar{y} \,\,$ represents the first moment of an area of the shaded section about N.A. in mm³ which we will denote as $\,\, Q \,\,$ , then