For cantilever beam BD
From Case No. 1 of
beam loading cases, the maximum deflection at the end of cantilever beam due to concentrated force at the free end is given by
$\delta = \dfrac{PL^3}{3EI}$
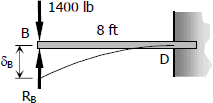Thus,
$\delta_B = \dfrac{1400(8^3)}{3EI} - \dfrac{R_B(8^3)}{3EI}$
$\delta_B = \dfrac{716\,800}{3EI} - \dfrac{512R_B}{3EI}$
For the simple beam AC
The deflection at distance x from Case No. 7 of different beam loadings is
$EI \, y = \dfrac{Pbx}{6L}(L^2 – x^2 – b^2)$ for $0 \lt x \lt a$
For $x = a$, the deflection equation will become
$EI \, y = \dfrac{Pab}{6L}(L^2 – a^2 – b^2)$
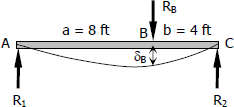For beam AC; P = RB, a = 8 ft, b = 4 ft, and L = 12 ft.
$\delta_B = \dfrac{R_B(8)(4)}{6(12)EI}(12^2 – 8^2 – 4^2)$
$\delta_B = \dfrac{4R_B}{9EI}(64)$
$\delta_B = \dfrac{256R_B}{9EI}$
Solving for the contact force, RB
$\delta_B = \delta_B$
$\dfrac{716\,800}{3EI} - \dfrac{512R_B}{3EI} = \dfrac{256R_B}{9EI}$
$\dfrac{716\,800}{3EI} = \dfrac{1972R_B}{9EI}$
$R_B = 1200 \, \text{ lb}$
Determining the maximum moment
The maximum moment on cantilever beam will occur at D
$M_D = 1200(8) – 1400(8)$
$M_D = –1600 \, \text{ lb}\cdot\text{ft}$
The maximum moment on simple beam will occur at point B.
$M_B = \dfrac{Pab}{L} = \dfrac{1200(8)(4)}{12}$
$M_B = 3200 \, \text{ lb}\cdot\text{ft}$
Maximum moment is at point B
$M_{max} = 3200 \, \text{ lb}\cdot\text{ft}$
Solving for maximum flexural stress
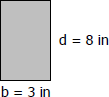The bending stress of rectangular beam is given by
$f_b = \dfrac{6M}{bd^2}$
Thus,
$( \, f_b \, )_{max} = \dfrac{6(3200)(12)}{3(8^2)}$
$( \, f_b \, )_{max} = 1200 \, \text{ psi} \,$ answer
